Загадка зниклого квадрата

На малюнку зображено дві фігури. Кожна з фігур складається з одних і тих же деталей. Порядок розташування деталей, як відомо, не впливає на загальну площу фігури. Куди пропав квадратик на нижньому малюнку?

 Відповідь:

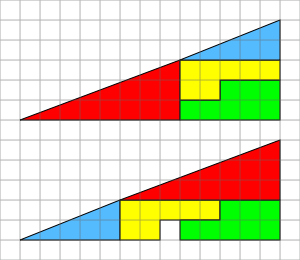
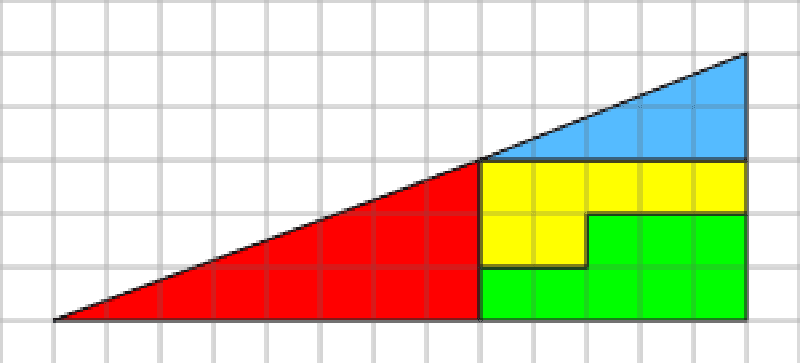
[hidepost]Ключем до загадки є те, що жодний із 13х5 «трикутників» не має ту ж саму площу, що й площа їх складових.

Сумарна площа чотирьох фігур (жовтої, червоної, синьої та зеленої) становить 32 одиниці площі, але довжини сторін трикутників 13 та 5, що відповідно становить 32,5 квадратних одиниць. Відношення катетів синього трикутника 5:2, а червоного 8:3. За ознакою подібності прямокутних трикутників випливає що ці трикутники не подібні, а значить мають різні відповідні гострі кути. Отже, видимі складені «гіпотенузи» великих «трикутників», насправді є ламаними.

Кут нахилу гіпотенуз червоного та синього трикутників до гіпотенузи 13х5 трикутника дуже малий і його важко помітити неозброєним оком. Але якщо приглядітись, то видно, що точка стику гіпотенуз червоного та синього трикутників, формує тупий кут, що трішки вигнутий вгору (назовні) нижнього «трикутника» і тупий кут вигнутий вниз (всередину) верхнього «трикутника». Якщо накласти «гіпотенузи» обох фігур, то утвориться паралелограм, площею рівною одному квадратику.[/hidepost]